El problema P vs NP es uno de los grandes problemas en el mundo de las matemáticas aplicadas y la informática, o más precisamente en la teoría de la complejidad computacional. A pesar de que sus bases teóricas se remontan a Alan Turing, fue planteado paralelamente en los años 70, por los programadores Stephen Cook y Leonid Levin, convirtiéndose en uno de los “problemas del milenio” del famoso Instituto Clay de Matemáticas, que ofrece una recompensa de un millón de dólares a quien pueda solucionarlo. Sin embargo, ¿de qué trata el problema y cuál es su complejidad? ¿por qué es relevante o importante? ¿existe forma de resolverlo?
En este artículo, queremos ofrecerte respuestas a estas preguntas en dos partes bien diferenciadas. La primera, donde encontraras en lenguaje divulgativo los elementos más importantes que definen el problema, su complejidad e importancia y, la segunda, que contiene la propuesta realizada por el autor, de un algoritmo de solución para el problema de la suma de subconjuntos -perteneciente a la subclase NP Completo– que satisface necesaria y suficientemente la igualdad P= NP.
Dejamos a la valoración crítica de todos y todas, especialmente de la comunidad científica versada en la temática, los hallazgos producidos en nuestra investigación.
La complejidad del problema del milenio P vs NP
El problema P vs NP es una de las preguntas más importantes en el campo de las ciencias de la computación, debido a las grandes repercusiones que habría, en caso de encontrarse una solución.
Su complejidad, esta relacionada con la TCC (teoría de la complejidad computacional), puesto que esta teoría -en sentido bastante simplificado-, persigue clasificar los problemas en aquellos que pueden o no ser resueltos con una cantidad determinada de recursos.
Estos recursos para efectos de dicha teoría son, tiempo y memoria. Es decir, el tiempo empleado durante determinado cálculo para resolver un problema dado y la memoria requerida para almacenar y procesar los datos del problema.
En nuestro mundo actual, sería sencillo suponer por intuición o lógica, que todos los problemas que se presenten a un ordenador pueden ser resueltos a pesar de cuán complejos sean. Pero, ¿es realmente así?
Resulta que en las matemáticas, al igual que en la informática, existen problemas que pueden o no tener solución, así mismo, en caso de existir alguna solución deben ser verificados, y esta requiere una utilización eficiente de recursos (tiempo y memoria) a través de algoritmos óptimos, donde preferiblemente no se disponga de millones de años para solucionarlos.
Una forma práctica de imaginar el universo computacional y su complejidad así como su relación con el problema P vs NP (que explicaremos más adelante) es intentar ordenar y resolver un puzzle (rompecabezas). El puzzle aumentará su complejidad en la medida que se añadan más y más piezas, y por tanto el tiempo empleado para resolverlo podría llegar a ser abrumador; ¿pero, si existiera un algoritmo capaz de ordenar aquellas piezas en la menor cantidad de tiempo (tiempo polinómico= podría interpretarse como rápidez)?- ¿sería eso una solución al problema del puzzle? -Y ¿cómo lo comprobaríamos?- Su verificación para este ejemplo quizás sea más sencilla, ver un puzzle completo y resuelto es más simple que ordenar cada una de sus piezas; o como opinaba Stephen Cook,… “hay problemas que sí pueden ser resueltos por un ordenador, solo que la máquina tardaría tanto, que el sol moriría antes”.
Así que el problema P vs NP, es algo más que un rompecabezas matemático abstracto. Su objetivo es determinar qué tipos de problemas se pueden resolver con ordenadores y cuáles no.
Si diluimos esta relación, encontraremos que los problemas de clase “P” (de sus siglas en inglés «tiempo polinomial) , son “fáciles” de resolver para los ordenadores, es decir, las soluciones a estos problemas pueden ser calculadas en una cantidad de tiempo razonable, en comparación con la complejidad del problema. Por ejemplo, 22, es un problema P, todos podemos resolverlo en un tiempo considerablemente rápido (orden polinómico). Así que, aquellos problemas que podemos solucionar y verificar con un algoritmo de orden polinómico, lo llamaremos problema P.
No sucede así, para su entrañable relación con “NP” (de sus siglas en inglés “tiempo no determinista polinomial”), aquí su solución podría ser muy “difícil” de encontrar, quizá requeriría miles de millones de años de computación, pero una vez encontrada, es fácil de comprobar.
Esta clase de problema, es decir NP, se encuentran en un limbo informático en el que son considerados como ejercicios sin solución (indecidibles) e irresolubles (intratables). Son la base de la seguridad del cifrado en criptografía , opera en modelos precisos de previsión financiera, en el análisis del comportamiento del pliegue de proteínas en una célula (como posible aplicación), y más cotidiano aún, en el juego SUDOKU, o en la búsqueda de horarios de vuelos aéreos.

Y luego está una relación aún más compleja, los problemas NP-Completos, que vienen siendo una especie de subclase a los NP ( es decir, están contenidos en la clase NP), estos se consideran problemas llave, porque si se encuentra una manera de resolver eficientemente solo uno (01) de ellos, significa que todos -todos los NP– pueden resolverse eficientemente. Así que los ordenadores actuales, tomarían especies de “atajos” para la resolución de dichos problemas, en caso de comprobarse su igualdad.
Ejemplos como el del viajero, persiguen explicar con mejor suficiencia este embrollo. Imagina que eres un comerciante que debe entregar paquetes de mercancías en varias ciudades -conociendo la distancia entre ellas- y necesitas la ruta más corta y eficiente para visitarlas una sola vez, sin repetir y volver a tu punto de origen. ¿Cuántas posibles rutas puedes calcular y en cuánto tiempo? ¿cuál es la más eficiente? En dicho ejemplo, las respuestas a las preguntas planteadas se pueden verificar, pero requieren un tiempo ridículamente largo e imposible para resolverlas mediante cualquier procedimiento directo.
Podríamos empezar por calcular cada una de las posibilidades, pero eso llevaría mucho tiempo, como ya hemos reforzado suficientemente. Así que, este problema lo que pretende demostrar es:
- ¿Es P diferente a NP?
- ¿Es P igual a NP?
El acervo científico actual nos dice que P es diferente a NP, pero no existe demostración alguna que corrobore ese planteamiento o lo contradiga. A no ser, que se empleen una serie de pasos, como un algoritmo lo suficientemente capaz de solucionar y demostrar que P es igual a NP. ¿Será esto posible?
Veamos paso a paso, cómo el desarrollo de la investigación nos plantea romper con el Santo Grial de las matemáticas, para beneficio de toda la comunidad científica a través de un algoritmo, que aporta una solución necesaria y suficiente a un problema NP-Completo, como lo es la suma de subconjuntos.
Un algoritmo de solución al problema NP- Completo
Recordemos que, el problema de la suma de subconjuntos pertenece a la categoría NP- completo (de acuerdo a la literatura científica existente) y su resolución- como problema llave- es equivalente a solucionar todos los de esta categoría. Para el desarrollo de dicho algoritmo- y su respectiva comprensión- iniciaremos con los siguientes enunciados, en forma de dos (02) planteamientos equivalentes, con el cual trabajaremos de ahora en adelante.
Planteamiento n°1:
Dado un conjunto de Enteros, ¿Existe algún subconjunto no vacío cuya suma sea exactamente igual a Cero?
Planteamiento n°2:
Dado un conjunto de Enteros y un Entero: S ¿Existe algún subconjunto cuya suma sea igual a: S?”
Ahora bien, si reducimos ese enunciado anterior, tenemos que:
Dado un conjunto de enteros: C cuya suma de sus elementos sea igual a: S” ¿Existe algún subconjunto: B perteneciente al conjunto: C cuya suma de los elementos del subconjunto: B sea igual a: S?
El próximo paso para llegar al algoritmo de solución, es diseñar dos criterios y certificados , que establezcan las condiciones necesarias y suficientes para tratar ambos planteamientos. El Criterio 1 permite abordar el Planteamiento 1 y el Criterio 2 tiene aplicación en el Planteamiento 2; la conjugación de ambos permite tratar el problema de la suma de subconjuntos.
Criterio 1: La condición necesaria y suficiente para que exista un subconjunto no vacío: B (Pero Nulo) perteneciente a un conjunto: A cuya suma sea igual a: S (A=S) Solo es necesario y suficiente que exista un subconjunto: C=S perteneciente al conjunto A, tal que: A – S = 0 y además que: A – C = 0
Para demostrar el funcionamiento del Criterio 1 tenemos que:
A = {-7 , -3 , -2 , 5 , 8} = 1
S = 1
C = {-7, 8} = 1
B = {-3 , -2 , 5} = 0
A – S = {-7 , -3 , -2 , 5 , 8 , -1} = 0
S = C = { -7 , -3 , -2 , 5 , 8 } = { -7 , 8 } = 1
Criterio 2: Para que exista un subconjunto no vacío ni nulo: C perteneciente a un conjunto: A cuya suma sea: S solo es necesario y suficiente que: A-C = B tal que: B sea un subconjunto no vacío ni nulo perteneciente a el conjunto: A
Un ejemplo, para el Criterio 2 es:
A = { -7 , -3 , -2 , 5 , 8 } = 1 A = { -7 , -3 , -2 , 5 , 8 } = 1
A = S = 1 A = S = 1
C = 4 C = 3
A – C = B = 1 – 4 = -3 A – C = B = 1 – 3 = -2
B = -3 B = -2
C = {5 , 8 , -7 , -2} = 4 C = {-2 , 5} = 3
Los criterios planteados, una vez analizados, sugieren un tratamiento efectivo al problema de la suma de subconjuntos, y esto nos permite, a su vez, proponer un pseudo código que logra transformar el problema de la suma de subconjuntos NP-completo a un problema NP y de igual forma de NP-completo a P. Presentamos pues, el siguiente algoritmo, el cual es ejecutable con lenguaje de programación Mat Lab R2020a.
Pseudocódigo del algoritmo Óptimo que permite demostrar que la suma de subconjunto está en: P
- t=cputime (Tiempo de ejecución)
- y=([10,-10,-5,16,-9]) (Conjunto de n elementos) (Entrada)
- s=sum(y) (Función Suma de n elementos)
- c=0 ó c=Cualquier entero (Constante o Parámetro de entrada)
- x1=([y(1)])(Cualquiera de los 2n-1 Subconjuntos propios de la entrada)
- sum(x1) (Función suma parcial del subconjunto propio)
- s==sum(x1) (Salida lógica de existencia y comparación)
- if ans==1 (Verificación y comprobación condicional (Criterio 1)
- A=([y(1)]) (Subconjunto)
- B=([y(2) y(3) y(4) y(5)]) (Subconjunto complementario)
- disp(‘Existe un subconjunto: B=S’)(Criterio 1)
- disp(‘Existe un subconjunto: A=0’)(Criterio 1)
- break (Detención de la ejecución o rutina)(Bucle anidado)
- else
- disp(‘No existe un subconjunto: B=S’)(Criterio 1)
- disp(‘No existe un subconjunto: A=0’)(Criterio 1)
- end (Fin)
- c==sum(x1) (Salida lógica de existencia y comparación)
- if ans==1 (Verificación y comprobación condicional) (Criterio 2)
- A=([y(1)])(Subconjunto)
- B=([y(2) y(3) y(4) y(5)]) (Subconjunto complementario)
- disp(‘Existe un subconjunto complementario: A1=0’)(Criterio 2)
- disp(‘Existe un subconjunto complementario: B=C’)(Criterio 2)
- break (Detención de la ejecución o rutina)(Bucle anidado)
- else
- disp(‘No existe un subconjunto: A=0’)(Criterio 2)
- disp(‘No existe un subconjunto: B=C’)(Criterio 2)
- end (Fin)
Fuente: Rodolfo Nieves (2022)
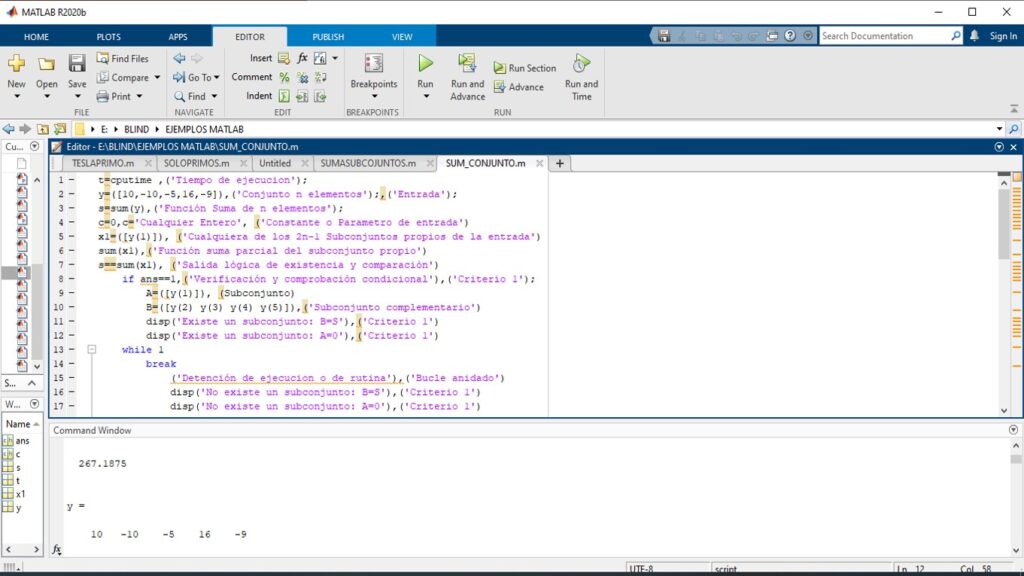
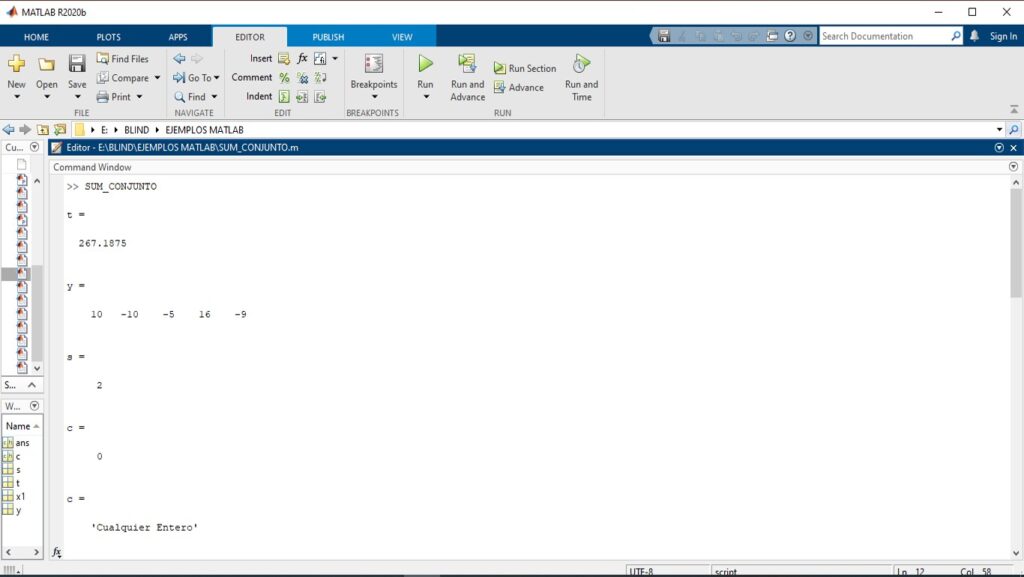
El cumplimiento de la ahora igualdad P=NP, a través del algoritmo presentado en el pseudo código, aporta una respuesta en orden polinómico al problema NP-completo, el cual invitamos sea evaluada, hasta en los espacios más escépticos. Por ahora, podemos agregar, que esperamos el pronunciamiento oficial del Instituto Clay sobre dicho algoritmo.
Después del algoritmo. ¿Qué sucederá?
Ciertamente no viviremos en otro universo -luego de la demostración suficiente y necesaria de dicho algoritmo- pero sí será posible quizás, estudiar a fondo algunas mutaciones en el ADN, o evaluar y hasta emular la forma en que se logran sintetizar algunas proteínas en nuestro organismo, entre otras diversas aplicaciones apasionantes y necesarias para nuestra sociedad. Una vez más, las matemáticas trascienden en otras áreas del conocimiento humano.
Para tener acceso al artículo científico original del Prof. Rodolfo Nieves, haz click aquí
Referencias bibliográficas
- Richard M. Karp (1972). «Reducibility Among Combinatorial Problems». En R. E. Millern and J. W. Thatcher (editors). Complexity of Computer Computations. New York: Plenum.pp. 85–103.
- Stephen Cook (1971). «The Complexity of Theorem Proving Procedures».Proceedings of the third annual ACM symposium on Theory of computing. pp. 151–158.
- David Zuckerman (1996). «On Unapproximable Versions of NP-Complete Problems».SIAM Journal on Computing25 (6): pp. 1293–1304. http://citeseer.ist.psu.edu/192662.html.
- G.B. Mathews, On the partition of numbers, Proceedings of the London Mathematical Society, 28:486-490, 1897.
- T. Cormen, C. Leiserson, R. Rivest. Introduction to Algorithms. MIT Press, 2001.pter 35.5, The subset-sum problem.
- Michael R. Garey and David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, 1979, W.H. Freeman. ISBN 0716710455 A3.2: SP13, pg.223.




